Calculate Effective Area

In this example we will calculate the effective area of a detector over a range of energies. This code can be run from the effective_area.py script in the examples directory.

Warning

In order to finish reasonably quickly, the number of events thrown in this example is low. This means that there are likely not enough events to accurately represent the effective area of the detector. For an accurate measurement, the number of events must be increased, but this will need much more time to run in that case. For the plots below, a higher number of events was thrown.

import numpy as np
import matplotlib.pyplot as plt
import pyrex
import pyrex.custom.ara as ara

# First let's set the number of events that we will be throwing at each energy,
# and the energies we will be using. As stated in the warning, the number of
# events is set low to speed up the example, but that means the results are
# likely inaccurate. The energies are high to increase the chance of triggering.
n_events = 100
energies = [1e9, 2e9, 5e9, 1e10] # GeV

# Next, set up the detector to be measured. Here we use a single standard
# ARA station.
detector = ara.RegularStation(x=0, y=0, antennas_per_string=4,
                              antenna_separation=[2, 18, 2])
detector.build_antennas(power_threshold=-6.15)

# Now set up a neutrino generator for each energy. We'll use unrealistically
# small volumes to increase the chance of triggering.
generators = [pyrex.CylindricalGenerator(dr=1000, dz=1000, energy=energy)
              for energy in energies]

# And then set up the event kernels for each energy.
kernels = [pyrex.EventKernel(generator=gen, antennas=detector)
           for gen in generators]

# Now run each kernel and record the number of events from each that triggered
# the detector. In this case we'll set our trigger condition to 3/8 antennas
# triggering in a single polarization.
triggers = np.zeros(len(energies))
for i, kernel in enumerate(kernels):
    print("Running energy", energies[i])
    for j in range(n_events):
        print(j, "..", sep="", end="")
        detector.clear(reset_noise=True)
        particle = kernel.event()
        triggered = detector.triggered(polarized_antenna_requirement=3)
        if triggered:
            triggers[i] += 1
            print("y", end=" ")
        else:
            print("n", end=" ")
        
        if j%10==9:
            print(flush=True)
    print(triggers[i], "events triggered at", energies[i]/1e6, "PeV")
print("Done")

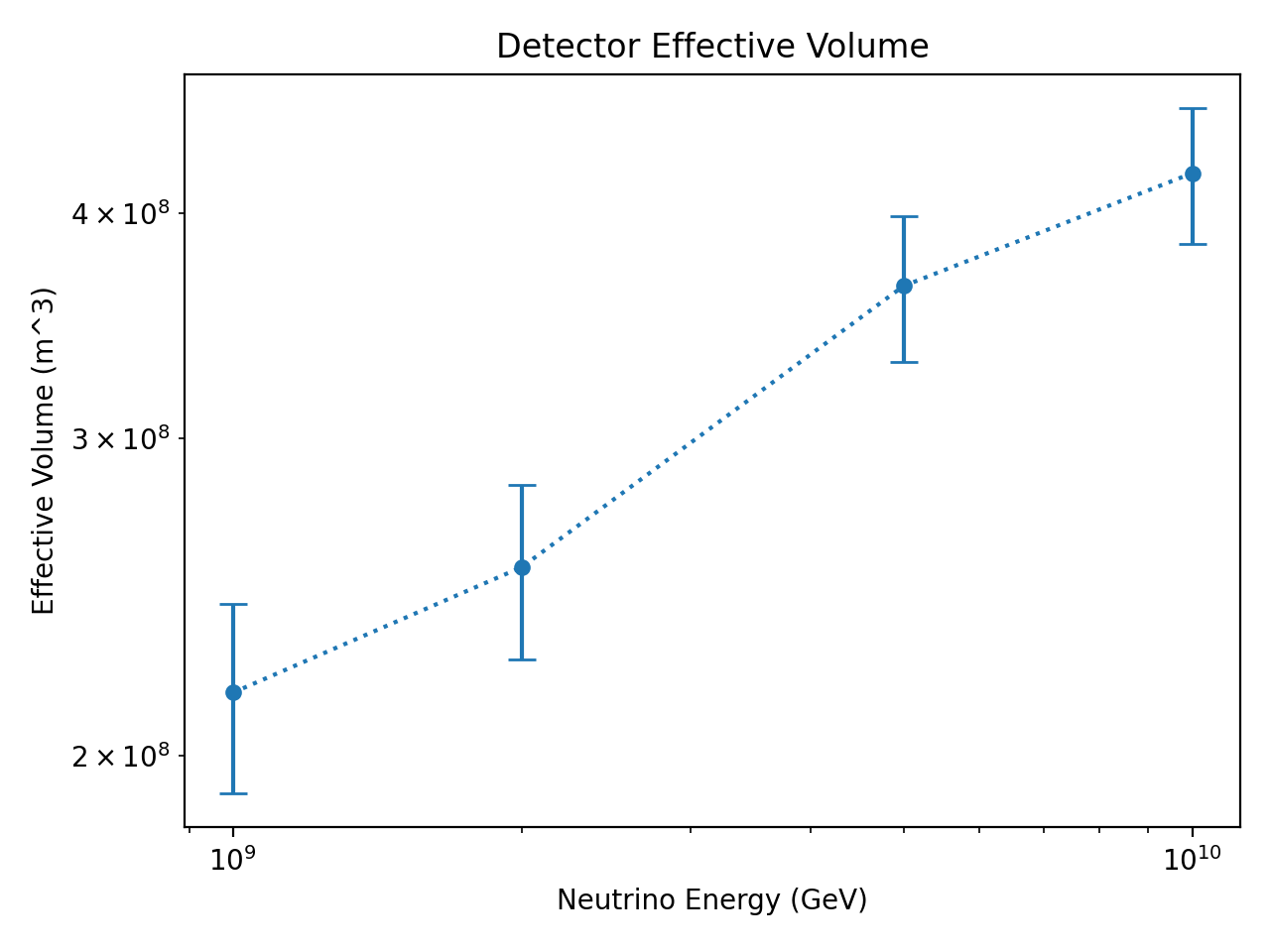
# Now that we have the trigger counts for each energy, we can calculate the
# effective volumes by scaling the trigger probability by the generation volume.
# Errors are calculated assuming poisson counting statistics.
generation_volumes = np.ones(4)*(np.pi*1000**2)*1000 # m^3
effective_volumes = triggers / n_events * generation_volumes
volume_errors = np.sqrt(triggers) / n_events * generation_volumes

plt.errorbar(energies, effective_volumes, yerr=volume_errors,
             marker="o", markersize=5, linestyle=":", capsize=5)
ax = plt.gca()
ax.set_xscale("log")
ax.set_yscale("log")
plt.title("Detector Effective Volume")
plt.xlabel("Neutrino Energy (GeV)")
plt.ylabel("Effective Volume (m^3)")
plt.tight_layout()
plt.show()

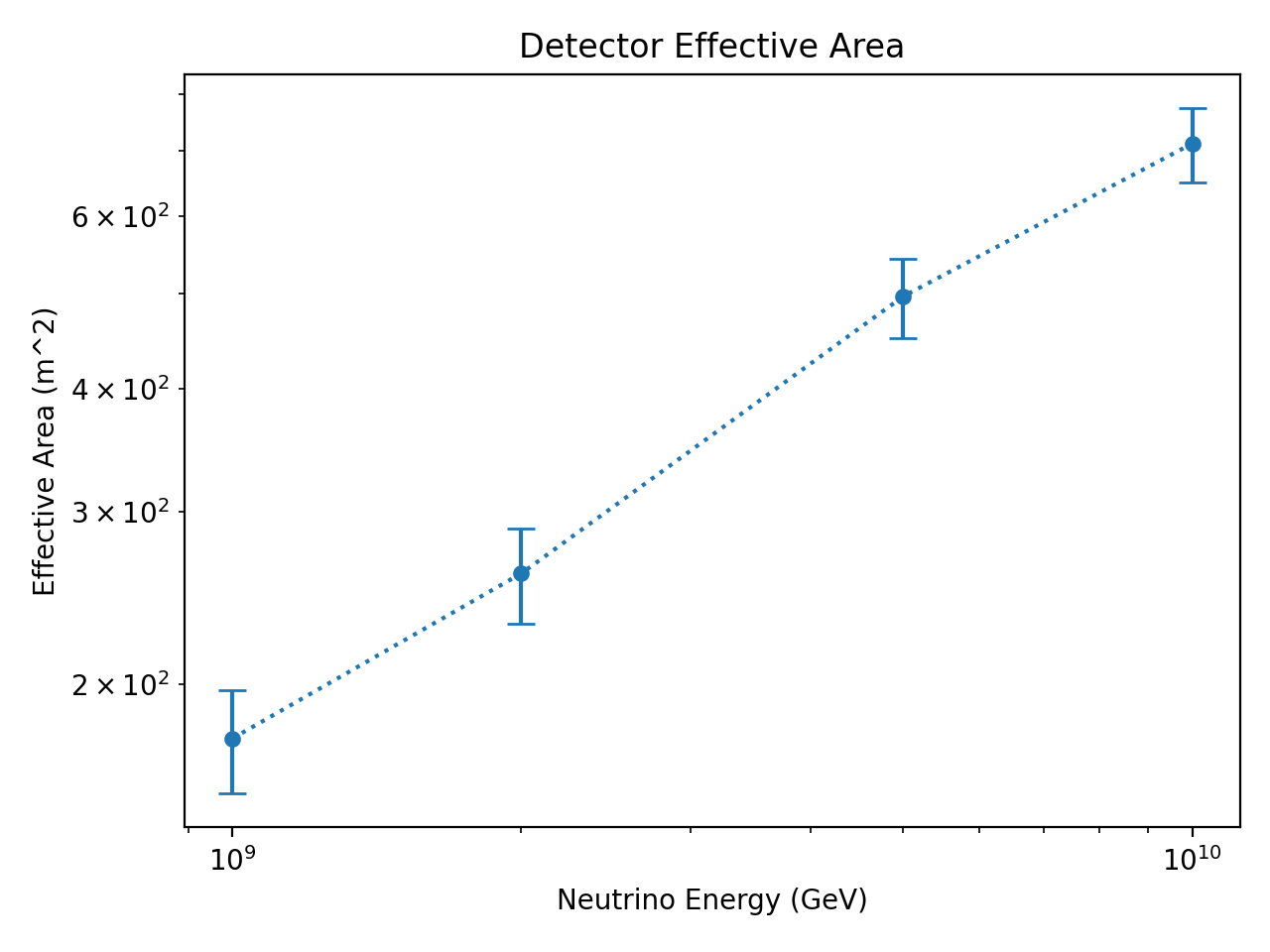
# Then from the effective volumes, we can calculate the effective areas.
# The effective area is given by the effective volume divided by the neutrino
# interaction length in the ice. The interaction length given by a PyREx
# Particle object is the water-equivalent interaction length, so it needs to
# be scaled by the relative density of ice. The interaction length used will
# be the harmonic mean of the neutrino and antineutrino interaction lengths
# (since the cross sections are what should be averaged).
int_lens = np.zeros(len(energies))
for i, energy in enumerate(energies):
    nu = pyrex.Particle(particle_id="nu_e", vertex=(0, 0, 0),
                        direction=(0, 0, 1), energy=energy)
    nu_bar = pyrex.Particle(particle_id="nu_e_bar", vertex=(0, 0, 0),
                            direction=(0, 0, 1), energy=energy)
    int_lens[i] = 2 / ((1/nu.interaction.total_interaction_length) +
                       (1/nu_bar.interaction.total_interaction_length))
int_lens *= 1e-2 # convert from cm to m (water-equivalent)
ice_density = 0.92 # g/cm^3, relative to 1 g/cm^3 for water
effective_areas = effective_volumes * ice_density / int_lens
area_errors = volume_errors * ice_density / int_lens

plt.errorbar(energies, effective_areas, yerr=area_errors,
             marker="o", markersize=5, linestyle=":", capsize=5)
ax = plt.gca()
ax.set_xscale("log")
ax.set_yscale("log")
plt.title("Detector Effective Area")
plt.xlabel("Neutrino Energy (GeV)")
plt.ylabel("Effective Area (m^2)")
plt.tight_layout()
plt.show()